Workshop 22. Graphs.¶

Graph is a set of related objects. The objects themselves are called vertices and their relations are called edges.

Here is a graph consisting of 6 numbered vertices and 7 edges.

Trees¶

A cycle is a graph (or a subgraph) in which vertices are connected in a cycle. For the example graph above, there are cycles [1-2-5], [1-2-3-4-5] and [2-3-4-5].

A graph without cycles is a tree.

Trees are commonly used in programming as a basis for a data structure, like a heap.

Adjacency matrix / adjacency list¶

Adjacency matrix is one of several ways to represent graph as a data structure.

It is a square matrix where each row and column represent a vertex, and the cells of the matrix represent the edge.

Here is the matrix for the graph above.

  | 1 2 3 4 5 6
--|------------
1 | 0 1 0 0 1 0
2 | 1 0 1 0 1 0
3 | 0 1 0 1 0 0
4 | 0 0 1 0 1 1
5 | 1 1 0 1 0 0
6 | 0 0 0 1 0 0

A similar approach is to use an adjacency list, where for each vertex a list of adjacent vertices is stored.

1 | [2, 5]
2 | [1, 3, 5]
3 | [2, 4]
4 | [3, 5, 6]
5 | [1, 2, 4]
6 | [4]

# Example of a program that converts an adjacency matrix into an adjacency list

adj_matrix = [
              [0, 0, 0, 1, 0, 0],
              [0, 0, 0, 1, 0, 0],
              [0, 0, 0, 1, 0, 0],
              [1, 1, 1, 0, 1, 0],
              [0, 0, 0, 1, 0, 1],
              [0, 0, 0, 0, 1, 0],
]

adj_list = []

for row in adj_matrix:
  new_row = []
  for i, x in enumerate(row):
    if x == 1:
      new_row.append(i)
  adj_list.append(new_row)

print(*adj_list, sep='\n')

[3]
[3]
[3]
[0, 1, 2, 4]
[3, 5]
[4]

Search algorithms¶

There are many algorithms related to graphs and trees, like finding the shortest path or finding the optimal way to cut the graph. Search algorithms are some of the basic ones.

There are two main search algorithms: breadth-first search and depth-first search.

Breadth-first search¶

In this algorithm, you first explore all the neighbor vertices of your known vertices before exploring the neighbors of the new ones.

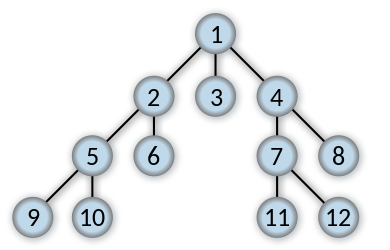
This illustration shows the order in which you would explore a graph using breadth-first search.

Depth-first search¶

In this algorithm, you first explore the neighbors of the newly found vertices, and only then process other known branches.

Implementation¶

# Breadth-first search


#            0
#         1  6  7
#      2  6     8  11
#  3   5        9  10

# Create a queue to store elements waiting to be processed
from collections import deque
queue = deque()

# Create an adjacency list correspoding to a tree from an illustration above
adj_list = [[1, 6, 7], [0, 2, 5], [1, 3, 4], [2], [2], [1], [0], [0, 8, 11],
            [7, 9, 10], [8], [8], [7]]

# Add the first element to the queue (the root)
queue.append(0)

# A set to save whether an element has been processed or not
processed = {0}

while queue:
  current_v = queue.popleft()
  print(current_v)
  for v in adj_list[current_v]:
    if v not in processed:
      queue.append(v)
      processed.add(v)
      # print(v)

0
7
11
8
10
9
6
1
5
2
4
3

Task 1¶

Change a single line in the above implementation, so it becomes a depth-first search instead of breadth-first one.

Task 2¶

Implement a recursive algorithm for depth-first search. Print the current vertex as in the example above. If implemented correctly, your algorithm should print the vertices in order: 0 1 2 3 4...

Task 2.1¶

Write a program that determines whether a graph is a tree or not.

processed = {0}

def DFS(adj_list, idx):

  for v in adj_list[idx]:
    if v not in processed:
      print(v)
      processed.add(v)
      DFS(adj_list, v)

DFS(adj_list, 0)
print(processed)

1
2
3
4
5
6
7
8
9
10
11
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

adj_list = [[1, 4],[0, 4],[1, 3],[2, 4, 5], [0, 1, 3],[3]]
flag = 1

appearances = {0}
for v in range(len(adj_list)):
    for v1 in range(len(adj_list[v])):
        if adj_list[v][v1] in appearances and v1 != 0:
            flag = 0
            break
        appearances.add(adj_list[v][v1])

if flag:
    print('It is a tree.')
else:
    print('It is not a tree.')

Task 3*¶

You are given a matrix which has numbers -1 and -2 as its elements.

a=[
[-1,-1,-1,-1,-1,-1,-1],
[-1,-2,-2,-2,-2,-1,-1],
[-1,-2,-2,-1,-1,-2,-1],
[-1,-2,-1,-2,-2,-2,-1],
[-1,-2,-2,-2,-2,-2,-1],
[-1,-2,-2,-1,-1,-1,-1],
[-1,-2,-2,-2,-2,-2,-1],
[-1,-1,-1,-1,-1,-1,-1]
]

-1 represents a wall (no cell)
-2 represents a cell

Convert this matrix into a graph where adjacent 4 cells become connected with an edge.

Part 1¶

Replace -1 with the number of the corresponding vertex

For example, for breadth-first search starting with the cell (4, 4), this is a possible order of the cells.

-1  -1  -1  -1  -1  -1  -1
-1  18  20  21  22  -1  -1
-1  17  19  -1  -1   5  -1
-1  10  -1   6   1   4  -1
-1   9   7   2   0  3   -1
-1  11   8  -1  -1  -1  -1
-1  12  13  14  15  16  -1
-1  -1  -1  -1  -1  -1  -1

Part 2¶

Create an adjacency list for the resulting graph.

The adjacency list for these cells is the following (vertex/cell numbers added for clarity):

(0, [1, 2, 3])
(1, [0, 6, 4])
(2, [6, 7, 0])
(3, [4, 0])
(4, [5, 3, 1])
(5, [4])
(6, [2, 1])
(7, [8, 9, 2])
(8, [7, 13, 11])
(9, [10, 11, 7])
(10, [17, 9])
(11, [9, 12, 8])
(12, [11, 13])
(13, [8, 12, 14])
(14, [13, 15])
(15, [14, 16])
(16, [15])
(17, [18, 10, 19])
(18, [17, 20])
(19, [20, 17])
(20, [19, 18, 21])
(21, [20, 22])
(22, [21])

from collections import deque

a=[
[-1,-1,-1,-1,-1,-1,-1],
[-1,-2,-2,-2,-2,-1,-1],
[-1,-2,-2,-1,-1,-2,-1],
[-1,-2,-1,-2,-2,-2,-1],
[-1,-2,-2,-2,-2,-2,-1],
[-1,-2,-2,-1,-1,-1,-1],
[-1,-2,-2,-2,-2,-2,-1],
[-1,-1,-1,-1,-1,-1,-1]
]