Workshop 17. Data structures

Stack

Stacks are collections of elements with two operations:

  • push(x) adds element x to the stack.
  • pop() removes the last added element from the stack and returns it.

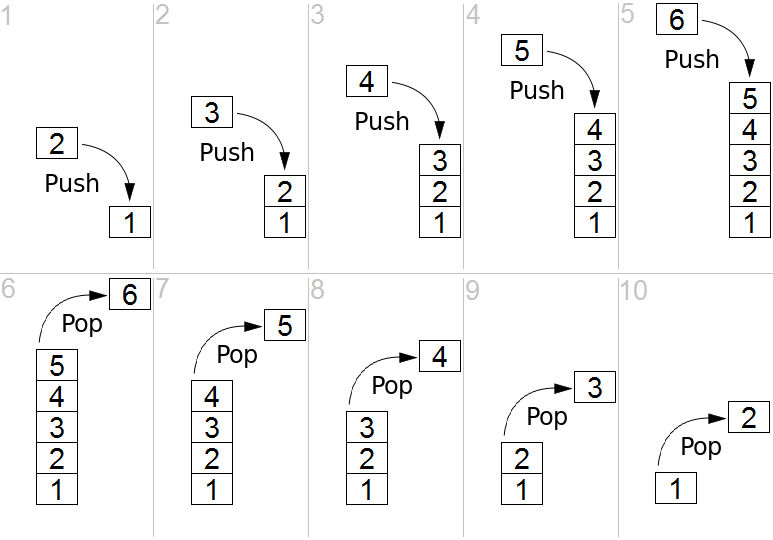
Stack

In [ ]:
# implementation of stacks using a list

stack = [3, 4, 5]
stack.append(6)
stack.append(7)
print(stack)

stack.pop()
print(stack)

stack.pop()
stack.pop()
print(stack)

[3, 4, 5, 6, 7]
[3, 4, 5, 6]
[3, 4]

Stacks are used to store the context of called functions, including recursive calls.

The error message for the following block of code will print the call stack of the functions.

In [2]:
def inner(x):
    raise ValueError
    return 1

def middle(x):
    return inner(x)

def outer(x):
    return middle(x)

outer(1)

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
/tmp/ipykernel_40872/588788785.py in <module>
      9     return middle(x)
     10 
---> 11 outer(1)

/tmp/ipykernel_40872/588788785.py in outer(x)
      7 
      8 def outer(x):
----> 9     return middle(x)
     10 
     11 outer(1)

/tmp/ipykernel_40872/588788785.py in middle(x)
      4 
      5 def middle(x):
----> 6     return inner(x)
      7 
      8 def outer(x):

/tmp/ipykernel_40872/588788785.py in inner(x)
      1 def inner(x):
----> 2     raise ValueError
      3     return 1
      4 
      5 def middle(x):

ValueError:

Queues

Queues are collections of elements with two operations:

  • push(x) adds element x to the end of the queue.
  • pop() removes the first element from the queue and returns it.

Queue

Queues can be implemented with a list but removing the first element from a list is an expensive operation, so such an implementation would be extremely unoptimized.

It is better to use collections.deque to implement a queue.

In [ ]:
from collections import deque
queue = deque([1, 2, 3])
print(queue)
queue.append(4)
queue.append(9)
print(queue)
print(queue.popleft())
print(queue)
print(queue.popleft())
print(queue.popleft())
print(queue)

deque([1, 2, 3])
deque([1, 2, 3, 4, 9])
1
deque([2, 3, 4, 9])
2
3
deque([4, 9])

The data type "queue" is used in many situations where a queue is expected naturally. For example, when multiple requests have to be processed, but only one can be processed at a time. Or, when processing an element means adding more elements for future processing, like in a breadth-first search.

Double-ended queue (deque)

Double-ended queue, or deque (pronounced deck) generalizes queue to allow four operations:

  • Add an element to the front of the deque
  • Add an element to the back of the deque
  • Remove an element from the front of the deque and return it
  • Remove an element from the back of the deque and return it
In [ ]:
from collections import deque
d = deque([10, 20, 50])   
for elem in d:    
    print(elem)
    
d.append('<-')     
d.appendleft('->')
print(d)

d.pop()           
d.popleft()       
list(d)

10
20
50
deque(['->', 10, 20, 50, '<-'])
Out[ ]:
[10, 20, 50]

Heap (priority queue)

Heap is a data structure represented as a binary tree where all child elements are greater (less) than or equal to the parent elements. Additionally, every "level" of the tree has to be full except for the lowest one.

It is possible to implement heaps as other types of trees which are more complex than binary ones.

A heap supports the following operations:

  • Add an element to the heap, while maintaining its structure.
  • Remove the root element from the heap, return it and reorganize the heap to maintain its structure.

Heap

Priority queue is an abstract data type similar to the regular queue. Its operations are:

  • Add an element with a certain priority to the queue.
  • Remove the element with the highest priority from the queue and return it.
  • Check if the queue is empty

Priority queues are ofter implemented with heaps.

In [ ]:
import heapq 
  
heap_list = [4, 10, 9, 1, 2] 
  
heapq.heapify(heap_list)
print(heap_list) 
  
heapq.heappush(heap_list, 5) 
print(heap_list) 
  
print(heapq.heappop(heap_list)) 

[1, 2, 9, 10, 4]
[1, 2, 5, 10, 4, 9]
1

A common way to implement heaps is to use lists, arrays or other linear data types, and maintain the following relationship between its elements:

a[k] <= a[2*k+1]' and 'a[k] <= a[2*k+2] for all k, counting elements from 0.

Heap as array

In [ ]:
# The order of elements in the array:

#                                0

#               1                                 2

#       3               4                5               6

#   7       8       9       10      11      12      13      14

# 15 16   17 18   19 20   21 22   23 24   25 26   27 28   29 30

The two operations can be combined for speed. There are two functions for doing this.

  • heappushpop first adds a new element, then pops the lowest one.
  • heapreplace first pops the lowest element, then adds a new one.
In [ ]:
heap_list_1 = [4, 10, 9, 1, 2]
heap_list_2 = [4, 10, 9, 1, 2]
  
heapq.heapify(heap_list_1) 
heapq.heapify(heap_list_2) 
  
print("headpushpop:")
print("Pushed 0")
print("Popped", heapq.heappushpop(heap_list_1, 0)) 
print(heap_list_1)
print()

print("heapreplace:")
print("Popped", heapq.heapreplace(heap_list_2, 0)) 
print("Pushed 0")
print(heap_list_2)

headpushpop:
Pushed 0
Popped 0
[1, 2, 9, 10, 4]

heapreplace:
Popped 1
Pushed 0
[0, 2, 9, 10, 4]

Task 1

Implement a function heapsort() that sorts iterables using a heap.

Use the module heapq.

Task 2. Fill

You are given a matrix as a list of lists.

a=[
[1,1,1,1,1,1,1],
[1,0,0,0,0,1,1],
[1,0,0,1,1,0,1],
[1,1,1,0,0,0,1],
[1,0,0,0,0,0,1],
[1,0,0,1,1,1,1],
[1,0,1,0,0,0,1],
[1,1,1,1,1,1,1]
]

Write a program that takes two coordinates x and y as input and "fills" the matrix with the value 2 using the following rules:

  • If the cell is 0, fill this cell and adjacent 4 cells (to the top, bottom, left and right).
  • If the cell is 1, do not fill the cell.
  • Use a queue.

Example:

Input: 4 4

Output:

1 1 1 1 1 1 1
1 0 0 0 0 1 1
1 0 0 1 1 2 1
1 1 1 2 2 2 1
1 2 2 2 2 2 1
1 2 2 1 1 1 1
1 2 1 0 0 0 1
1 1 1 1 1 1 1
In [ ]:
from collections import deque

a=[
[1,1,1,1,1,1,1],
[1,0,0,0,0,1,1],
[1,0,0,1,1,0,1],
[1,1,1,0,0,0,1],
[1,0,0,0,0,0,1],
[1,0,0,1,1,1,1],
[1,0,1,0,0,0,1],
[1,1,1,1,1,1,1]
]

Task 2.1 Loop Fill

Modify the solution of the previous task so that the filling process loops around the edges of the matrix.

In [ ]:
a=[
[1,0,1,1,1,1,1],
[1,0,0,0,0,1,1],
[1,0,0,1,1,0,1],
[1,1,1,0,0,0,1],
[1,0,0,0,0,0,1],
[1,0,0,1,1,1,1],
[1,0,1,0,0,0,1],
[1,0,1,1,1,1,1]
]

result = [
[1,2,1,1,1,1,1],
[1,2,2,2,2,1,1],
[1,2,2,1,1,2,1],
[1,1,1,2,2,2,1],
[1,2,2,2,2,2,1],
[1,2,2,1,1,1,1],
[1,2,1,0,0,0,1],
[1,2,1,1,1,1,1]
]